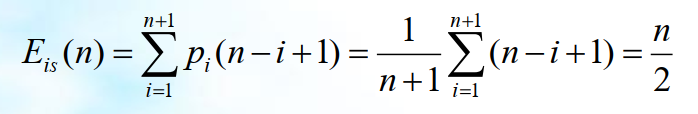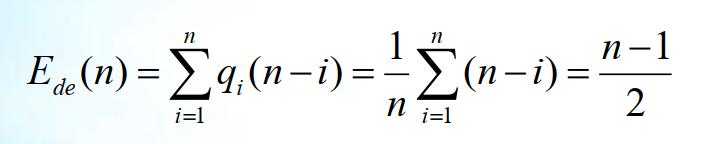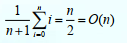首页 数据结构 精讲二 第二章 线性表
文章
取消

数据结构 精讲二 第二章 线性表

发表于 2023/08/02 更新于 2023/08/07
作者 睦mu
26 分钟阅读

数据结构 精讲二 第二章 线性表1

1 线性表的定义和基本运算

1.1. 线性表的逻辑定义

线性表（Linear List） 是最简单和最常用的一种数据结构， 它是由n个数据元素（结点） a~1~, a~2~, …a~n~如组成的有限序列。 其中， 数据元素的个数n为表的长度。 当n为零时称为空表， 非空的线性表通常记为

( a~1~, a~2~, …, a~i-1~, a~i~, a~i+1~, …, a~n~ )

这里的元素 a~i~(a≤i≤n)是一个抽象的符号， 它可以是一个数或者一个符号， 还可以是较复杂的记录。 如一个学生、 一本书等信息就是一个数据元素， 它可以由若干个数据项组成

image-20230802151209515

1.2. 线性表的基本运算

对于线性表，常见的基本运算有以下几种：

  1. 置空表InitList ( L )，构造一个空的线性表L。
  2. 求表长ListLength ( L )，返回线性表L中元素个数，即表长。
  3. 取表中第i个元素GetNode ( L, i )，若1≤i≤ListLength ( L )，则返回第i个元素a~i~。
  4. 按值查找LocateNode ( L, x )，在表L中查找第一个值为x的元素，并返回该元素在表L中的位置，若表中没有元素的值为x，则返回0值。
  5. 插入InsertList ( L, i, X )，在表L的第i元素之前插入一个值为x的新元素，表L的长度加1。
  6. 删除DeleteList ( L, i )，删除表L的第i个元素，表L的长度减1。

2 线性表的顺序存储和基本运算的实现

2.1 线性表的顺序存储

线性表的顺序存储指的是将线性表的数据元素按其逻辑次序依次存入一组地址连续的存储单元里，用这种方法存储的线性表称为顺序表。

假设线性表中所有元素的类型是相同的， 且每个元素需占用d个存储单元， 其中第一个单元的存储位置（地址） 就是该元素的存储位置。 那么， 线性表中第i+1个元素的存储位置LOC( a~i+1~ )和第i个元素的存储位置LOC( a~i~ )有关系：LOC( a~i+1~ )=LOC( a~i~ )+d

一般来说， 线性表的第i个元素A的存储位置为: LOC( a~i~ )=LOC( a~1~ )+( i-1)*d

其中， LOC(a~1~)是线性表的第一个元素a~1~的存储位置， 通常称之为基地址。

线性表的这种机内表示称为线性表的顺序存储结构。它的特点是， 元素在表中的相邻关系，在计算机内也存在着相邻的关系。

1
2
3
4
5
6

#define ListSize 100 //表空间的大小应根据实际需要来定义，这里假设为100
typedef int DataType; //DataType的类型可根据实际情况而定，这里假设为int
typedef struct {
    DataType data [ ListSize ]; //数组data用来存放表结点
    int length; //线性表的当前表长（实际存储元素的个数）
} SeqList;

image-20230802170112310

2.2 顺序表上基本运算的实现

  1. 插入运算

    • 概述

      线性表的插入运算是指在线性表的第i-1个元素和第i个元素之间插入一个新元素x，使长度为n的线性表：( a~1~, a~2~, …, a~i-1~, a~i~, …, a~n~ ) 变为长度为n+1的线性表：( a~1~, a~2~, …, a~i-1~, x, a~i~, …, a~n~ ) 由于线性表逻辑上相邻的元素在物理结构上也是相邻的，因此在插入一个新元素之后，线性表的逻辑关系发生了变化，其物理存储关系也要发生相应的变化。除非i=n+1，否则必须将原线性表的第i、 i+1、 …、 n个元素分别向后移动1个位置，空出第i个位置以便插入新元素x。

      1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

      void InsertList ( SeqList *L, int i, DataType x ){ //在顺序表L中第i个位置之前插入一个新元素x
    int j;
    if ( i<1 || i>L->length+1 ) {
        printf ( "position error");
        return;
    }
    if ( L->length>=ListSize) {
        printf ( "overflow" );
        return;
    }
    for ( j=L->length-1;j>=i-1; j--)
        L->data[ j+1]=L->data[j]; //从最后一个元素开始逐一后移
	L->data[ i-1]=x; //插入新元素x
	L->length++; //实际表长加1
}

    • 特点：

      一般情况下，在第i（1≤i≤n）个元素之前插入一个新元素时，需要进行n-i+1次移动。而该算法的执行时间主要花在for循环的元素后移上，因此该算法的时间复杂度不仅依赖于表的长度n，而且还与元素的插入位置i有关。 当i=n+1时， for循环一次也不执行，无需移动元素，属于最好情况，其时间复杂度为O(1)； 当i=1，循环需要执行n次，即需要移动表中所有元素，属于最坏情况，算法时间复杂度为O(n)。由于插入元素可在表的任何位置上进行，因此需要分析讨论算法的平均移动次数。 在等概率情况下插入，需要移动元素的平均次数为 ：

      image-20230802172329971

  2. 删除运算

    • 概述

      线性表的删除运算指的是将表中第i个元素删除，使长度为n的线性表：( a~1~, a~2~, …, a~i-1~, a~i~, a~i+1~, …, a~n~ ) 变为长度为n-1的线性表：( a~1~, a~2~, …, a~i-1~, a~i+1~, …, a~n~ ) 线性表的逻辑结构和存储结构都发生了相应的变化，与插入运算相反， 插入是向后移动元素，而删除运算则是向前移动元素，除非i=n时直接删除 终端元素，不需移动元素。

      1
2
3
4
5
6
7
8
9
10
11
12
13

      DataType DeleteList ( SeqList *L, int i ){ //在顺序表L中删除第i个元素， 并返回被删除元素
    int j;
    DataType x; //DataType是一个通用类型标识符， 在使用时再定义实际类型
    if ( i<1 || i>L->length ) {
        printf ( "position error" );
        exit ( 0 ); //出错退出处理
    }
    x=L->data [ i-1 ]; //保存被删除元素
    for ( j=i; j<=L->length; j++)
        L->data[j-1]=L->data[ j ]; //元素前移
    L->length--; //实际表长减1
    return x; //返回被删除的元素
}

    • 特点

      该算法的时间复杂度分析与插入算法类似， 删除一个元素也需要移动元素， 移动的次数取决于表长n和位置i。 当i=1时， 则前移n-1次； 当i=n时不需要移动， 因此算法的时间复杂度为O(n)。 由于算法中删除第i个元素是将从第i+1至第n个元素依次向前移动一个位置， 共需要移动n-i个元素。 同插入类似， 假设在顺序表上删除任何位置上元素的机会相等， q~i~为删除第i个元素的概率， 则删除一个元素的平均移动次数为：

      image-20230802173022401

      在顺序表上做删除运算，平均移动元素次数约为表长的一半，因此该算法的平均时间复杂度为O(n)。

3 线性表的链式存储结构

线性表顺序存储结构

的特点是， 在逻辑关系上相邻的两个元素在物理位置上也是相邻的， 因此可以随机存取表中任一元素。 但是， 当经常需要做插入和删除操作运算时， 则需要移动大量的元素， 而采用链式存储结构时就可以避免这些移动。 然而， 由于链式存储结构存储线性表数据元素的存储空间可能是连续的， 也可能是不连续的， 因而链表的结点是不可以随机存取的

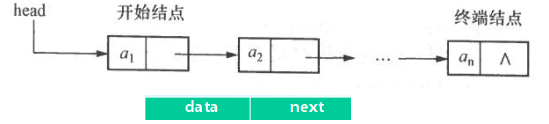
3.1. 单链表

  1. 概述

    image-20230803154053456

    1
2
3
4
5
6
7

    typedef struct node { //结点类型定义
    DataType data ; //结点数据域
    struct node * next ; //结点指针域
} ListNode;
typedef ListNode * LinkList ;
ListNode * p ; //定义一个指向结点的指针变量
LinkList head ; //定义指向单链表的头指针

  2. 单链表上的基本运算

    • 建立单键表

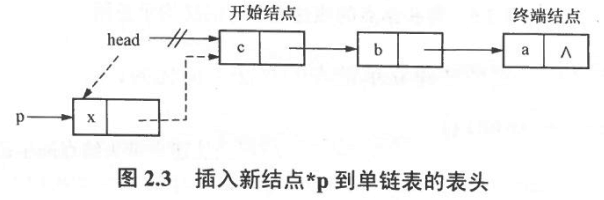
      • 头插法建表：头插法建表是从一个空表开始， 重复读入数据， 生成新结点， 将读入的数据存放到新结点的数据域中， 然后将新结点插入到当前链表的表头上， 直到读入结束标志为止。 假设线性表中结点的数据域为字符型

        image-20230803154529213

        1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

        LinkList CreateListF ( ){ 
    LinkList head;
    ListNode *p ;
    char ch ;
    head=NULL; //置空单链表
    ch=getchar ( ) ; //读入第一个字符
    while ( ch!='\n') { //读入字符不是结束标志符时作循环
        p= ( ListNode * ) malloc (sizeof ( ListNode ) ) ;//申请新结点
        p->data=ch; //数据域赋值
        p->next=head; //指针域赋值
        head=p; //头指针指向新结点
        ch=getchar ( ) ; //读入下一个字符
    }
    return head; //返回链表的头指针
}

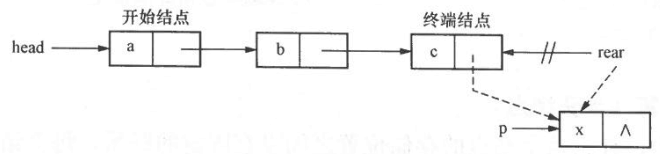
      • 尾插法建表

        image-20230803154845971

        1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

        LinkList CreateListR ( ){ 
    LinkList head, rear;
    ListNode *p ;
    char ch ;
    head=NULL; rear=NULL; //置空单链表
    ch=getchar ( ) ; //读入第一个字符
    while ( ch!=‘\n’ ) { //读入字符不是结束标志符时作循环
        p= ( ListNode * ) malloc ( sizeof ( ListNode ) ) ; //申请新结点
        p->data=ch ; //数据域赋值
        if ( head==NULL ) head=p ; //新结点*p插入空表
        else rear->next=p ; //新结点*p插入到非空表的表为结点*rear之后
        rear=p; //表尾指针指向新的表尾结点
        ch=getchar ( ) ; //读入下一个字符
    }
    if ( rear!=NULL ) rear->next=NULL ; //终端结点指针域置空
    return head ;
}

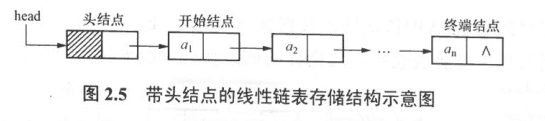
      • 为了简化算法，方便操作，可在链表的开始结点之前附加一个结点，并称其为头结点。带头结点的单链表结构

        image-20230807171504480

        1
2
3
4
5
6
7
8
9
10
11
12
13
14

        LinkList CreateListR1 ( ){ //尾插法建立带头结点的单链表算法
    LinkList head= ( ListNode * ) malloc (sizeof ( ListNode ) ); //申请头结点
    ListNode *p, *r ;
    DataType ch ;
    r=head ; //尾指针初始指向头结点
    while ( ( ch=getchar ( ) ) !=‘\n’ ) {
        p= ( ListNode * ) malloc ( sizeof ( ListNode ) ) ; //申请新结点
        p->data=ch ;
        r->next=p; //新结点连接到尾结点之后
        r=p ; //尾指针指向新结点
    }
    r->next=NULL; //终端结点指针域置空
    return head;
}

    • 查找运算（带头结点）

      • 按结点序号查找 ：在单链表中要查找第i个结点，就必须从链表的第1个结点（开始结点，序号为1）开始，序号为0的是头结点， P指向当前结点， j为计数器，其初始值为1，当p扫描下一个结点时，计数器加1。当j=i 时，指针P所指向的结点就是要找的结点

        在等概率情况下，平均时间复杂度为

        image-20230807172319866

        1
2
3
4
5
6
7
8
9
10
11
12

        ListNode * GetNodei ( LinkList head, int i ){ //head为带头结点的单链表的头指针， i为要查找的结点序号;若查找成功，则返回查找结点的存储地址（位置），否则返回NULL
    ListNode *p; int j ;
    p=head->next ; j=1 ; //使p指向第一个结点， j置1
    while ( p!=NULL && j<i ) { //顺指针向后查找，直到p指向第i个结点或p为空为止
        p=p->next ;
        ++j ;
    }
    if ( j==i )
        return p;
    else
        return NULL;
}

      • 按结点值查找 ：在单链表中按值查找结点， 就是从链表的开始结点出发， 顺链逐个将结点的值和给定值k进行比较， 若遇到相等的值， 则返回该结点的存储位置， 否则返回NULL。 按值查找算法要比按序号查找更为简单

        该算法的时间主要花在查找操作上，循环最坏情况下执行n次，因此其算法时间复杂度为O(n) 

        1
2
3
4
5
6

        ListNode * LocateNodek ( LinkList head, DataType k ){ //head为带头结点的单链表的头指针， k为要查找的结点值;若查找成功， 则返回查找结点的存储地址（位置） ， 否则返回NULL
    ListNode *p=head->next ; //p指向开始结点
    while ( p!=Null && p->data!=k ) //循环直到p等于NULL或p->data等于k为止
        p=p->next ; //指针指向下一个结点
    return p; //若找到值为k的结点， 则p指向该结点， 否则p为 NULL
}

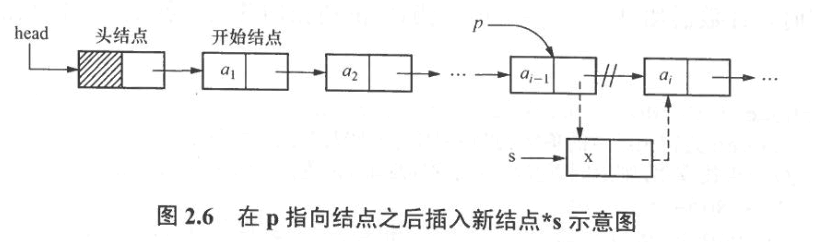
    • 插入运算：插入算法不需要移动表结点，但为了使p指向第i-1个结点，仍然需要从表头开始进行查找，因此该插入算法的时间复杂度也是O(n)

      image-20230802181041543

      1
2
3
4
5
6
7
8
9
10
11
12
13
14

      void InsertList ( LinkList head, int i, DataType x ){ //在以head为头指针的带头结点的单链表中第i个结点的位置上插入一个数据域值为x的新结点
    ListNode *p, *s; int j ;
    p=head ; j=0 ;
    while (p!=NULL && j<i-1 ) { //使p指向第i-1个结点
        p=p->next ; ++j；
    }
    if ( p==NULL ) { //插入位置错误
        printf ( "ERROR\n") ; return ;
    } else {
        s= ( ListNode * ) malloc ( sizeof ( ListNode );//申请新结点
		s->data=x ; s->next=p->next ;
		p->next=s ;
	}
}

    • 删除运算

      删除算法与插入算法的时间复杂度一样，都是O(n)

      image-20230803150625312

      1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

      DataType DeleteList ( LinkList head , int i ){ //在以head为头指针的带头结点的单链表中删除第i个结点
    ListNode *p , *s ;
    DataType x ; int j ;
    p=head ; j=0 ;
    while ( p!=NULL && j<i-1) { //使p指向第i-1个结点
        p=p->next ; ++j ;
    }
    if ( p==NULL ) { //删除位置错误
        printf ( "位置错误\n" ) ;
        exit ( 0 ) ; //出错退出处理
    }else {
        s=p->next ; //s指向第i个结点
        p->next=s->next ; //使p->next指向第i+1个结点
        x=s->data ; //保存被删除结点的值
        free ( s ) ; return x ; //删除第i个结点， 返回结点
    }
}

3.1 循环链表

循环链表的结点类型与单链表完全相同，在操作上也与单链表基本一致，差别仅在于算法中循环的结束判断条件不再是p或p->next是否为空，而是它们是否等于头指针。

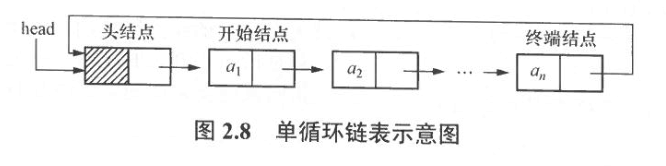
image-20230807173959159

在用头指针表示的单循环链表中，查找任何结点都必须从开始结点查起，而在实际应用中，表的操作常常会在表尾进行，此时若用尾指针表示单循环链表，可使某些操作简化。

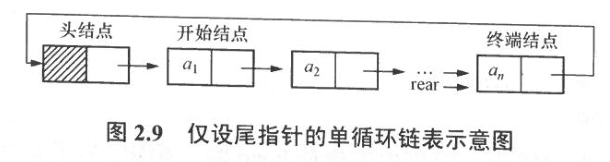
image-20230807174008424

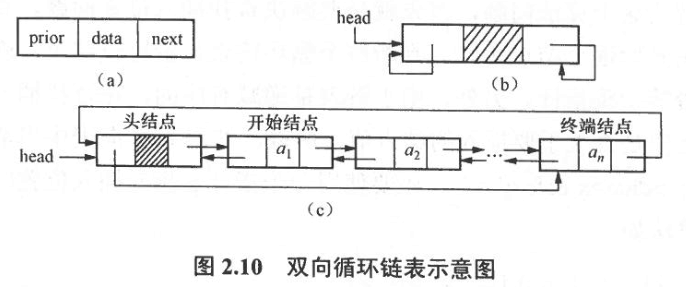
3.2 双向链表

image-20230807181312014

1
2
3
4
5
6

typedef struct dlnode {
    DataType data ;
    struct dlnode *prior , *next ;
} DLNode ;
typedef DLNode * DLinkList ;
DlinkList head ;

3.2.1. 双向链表的插入与删除

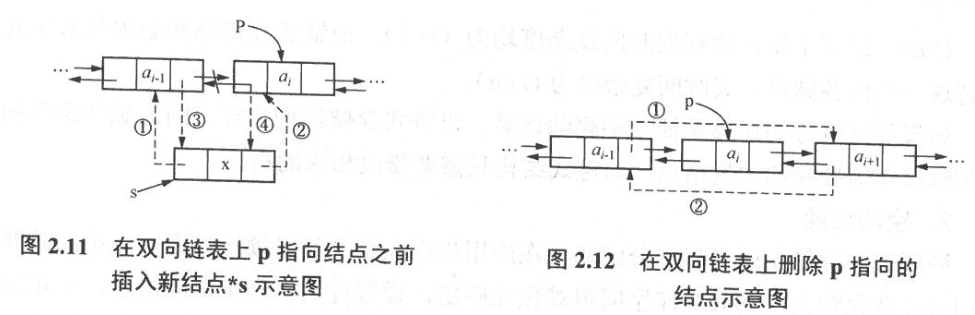
在双向链表的给定结点前插入一结点的操作过程如图2.11所示。设p为给定结点的指针， x为待插入结点的值

image-20230807182002247

1
2
3
4
5
6

void DLInsert ( DLNode *p , DataType x ){ //将值为x的新结点插入到带头结点的双向链表中指定结点*p之前
    DLNode *s= ( DLNode * ) malloc ( sizeof ( DLNode ) ) ; //申请新结点
    s->data=x ;
    s->prior=p->prior ; s->next=p ;
    p->prior->next=s ; p->prior=s ;
}

因为不再需要查找指向删除结点的前趋结点的指针，所以在双向链表上删除指定结点*p的算法更为简单，其删除操作过程如图2.12所示

1
2
3
4
5
6
7

DataType DLDelete ( DLNode *p ){ //删除带头结点的双向链表中指定结点*p
    p->prior->next=p->next:
    p->next->prior=p->prior ;
    x=p->data ;
    free ( p ) ;
    return x ;
}

4 顺序表和链表的比较

4.1. 时间性能

如果在实际问题中， 对线性表的操作是经常性的查找运算， 以顺序表形式存储为宜。 因为顺序存储是一种随机存取结构， 可以随机访问任一结点， 访问每个结点的时间代价是一样的， 即每个结点的存取时间复杂度均为O(1)。 而链式存储结构必须从表头开始沿链逐一访问各结点， 其时间复杂度为O(n)。 如果经常进行的运算是插入和删除运算，以链式存储结构为宜。因为顺序表作 插入和删除操作需要移动大量结点，而链式结构只需要修改相应的指针

4.2. 空间性能

顺序表的存储空间是静态分配的， 在应用程序执行之前必须给定空间大小。 若线性表的长度变化较大， 则其存储空间很难预先确定， 设置过大将产生空间浪费， 设定过小会使空间溢出， 因此对数据量大小能事先知道的应用问题， 适合使用顺序存储结构。 而链式存储是动态分配存储空间， 只要内存有空闲空间， 就不会产生溢出， 因此对数据量变化较大的动态问题， 以链式存储结构为好。 对于线性表结点的存储密度问题， 也是选择存储结构的一个重要依据。 所谓存储密度 就是结点空间的利用率。 它的计算公式为 存储密度=( 结点数据域所占空间） / ( 整个结点所占空间） —般来说，结点存储密度越大，存储空间的利用率就越高。显然， 顺序表结点的存储密度是1，而链表结点的存储密度肯定小于1。例如，若单链表结点数据域为整型数，指针所占的存储空间和整型数相同，则其结点的存储密度为50%。因此，若不考虑顺序表的空闲区，则顺序表的存储空间利用率为100%，远高于单链表的结点存储密度

image-20230802175950167

  1. 尚德机构 ↩ ↩

sunlands, 数据结构 精讲二 第二章 线性表
sunlands 数据结构 线性表
本文由作者按照 CC BY 4.0 进行授权
最近更新
文章内容

操作系统 第一章 操作系统概论

数据结构 第三章 栈和队列