数据结构 第四章 多维数组和广义表

数据结构 精讲六 第四章 多维数组和广义表 ¹

1 多维数组和运算

1.1. 数组的顺序存储

二维数组又可以以行向量形式表示为：

A~m×n~=[[a~00~, a~01~, … ,a~0 n-1~], [a~10~, a~11~, …, a~1~ ~n-1~], …, [a~m-1~ ~0~, a~m-1~ ~1~, …, a~m-1~ ~n-1~]]

或者以列向量形式表示为: A~m×n~=[[a~00~, a~10~, … ,a~m-1~ ~0~], [a~01~, a~11~, …, a~m-1~ ~1~], …, [a~0~ ~n-1~, a~1~ ~n-1~, …, a~m-1~ ~n-1~]] 多维数组是一种复杂的数据结构。以二维数组为例，数组元素之间的关系除了边界元素外，每个元素a~ij~都恰好有两个直接前趋和两个直接后继：行向量上的直接前趋是a~ij-1~和a~ij+1~，列向量上的直接前趋是a~i-1j~和直接后继叫a~i+1j~。并且二维数组也只有一个开始结点a~00~，它没有前趋；仅有一个终端结点a~m-1~ ~n-1~它没有后继。此外，边界上的结点（开始结点和终端结点除外）只有一个直接前趋或者只有一个直接后继。

数组在各种高级语言中通常也有两种不同的顺序存储方式，其中最典型的Pascal和C语言是按行优先顺序存储的，而Fortran语言则是按列优先顺序存储的。

1. 按行优先顺序存储，即将数组元素按行向量排列，第i+1个行向量紧接在第i个行向量后面。 A的m×n个元素按行优先顺序存储的线性序列为： a~00~, a~01~, … ,a~0~ ~n-1~, a~10~, a~11~, …, a~1~ ~n-1~, a~m-1~ ~0~, a~m-1~ ~1~, …, a~m-1~ ~n-1~
2. 按列优先顺序存储，即将数组元素按列向量排列，第j+1个列向量紧接在第j个列向量之后， A的m×n个元素按列优先顺序存储的线性序列为： a~00~, a~10~, … ,a~m-1~ ~0~, a~01~, a~11~, …, a~m-1~ ~1~, a~0~ ~n-1~, a~1~ ~n-1~, …, a~m-1~ ~n-1~

二维数组A~m×n~按行优先顺序存储在内存中，假设每个元素占d个存储单元，数组元素a~ij~( i=0, 1, …, m-1; j=0, 1, …, n-1 )位于第i行、第j列，前面i行共有i×n个元素，第i行上a~ij~前面又有j个元素，因此它的前面一共有i×n+j个元素，所以在C语言中的数组元素a~ij~的地址计算函数为：

LOC(a~ij~)=LOC(a~00~)+(i×n+j)×d

例如，有数组A~4×5~, d=2，LOC(a~00~)=100，计算a~23~的存储地址。 因为i=2，j=3，n=5，根据地址计算函数得： LOC(a~23~)=100+(2×5+3)×2=126 同理，三维数组A~m×n×p~按行优先顺序在内存中，计算数组元素a~ijk~的地址计算函数为： LOC(a~ijk~)=LOC(a~000~)+(i×n×p+j×p+k)×d

1.2. 数组运算举例

例： 设计一个算法，实现矩阵A~mn~的转置矩阵取B~nm~。 分析：对于一个mxn的矩阵A，其转置矩阵是一个n×m的矩阵B，而且B[i][j]=A[j][i]，0≤i≤n-1， 0≤j≤m-1。假设m=5，n=8，其实现算法如下：

void trsmat ( int a[][8], int b[][5], int m, int n){
    int i, j;
    for(j=0; j<m; j++)
        for(i=0; i<n; i++)
            b[i][j]=a[j][i];
}

2 矩阵的压缩存储

在有些情况下，矩阵中含有许多值相同或者值为零的元素，如果还按前面的方法来存储这种矩阵，就会产生大量的空间浪费。为了节省存储空间，可以对这类矩阵采用压缩存储

2.1. 特殊矩阵

特殊矩阵，指的是相同值的元素或者零元素在矩阵中的分布有一定规律的矩阵。下面分别讨论几种特殊矩阵的压缩存储。

2.1.1. 对称矩阵

若n阶方阵A中的元素满足下述性质：

a~ij~=a~ji~ (0≤i，j≤n-1) 则称A为n阶的对称矩阵。对称矩阵中的元素是关于主对角线对称的，所以只需要存储矩阵上三角或下三角的元素即可，让两个对称的元素共享一个存储空间。这样，就能够节省近一半的存储空间。按C语言的“按行优先”存储主对角线（包括主对角线）以下的元素，如图4.2所示。

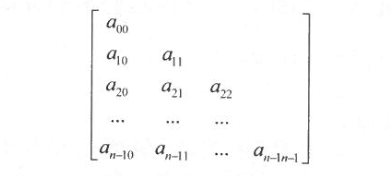
在以上的下三角矩阵中，第i行（0≤i≤n-1）恰好有i+1个元素，所以元素总数为：

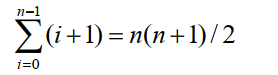
现假设以一维数组sa[n(n+1)/2]作为n阶对称矩阵A的存储结构，那么，矩阵中元素a~ij~和数组元素sa[k]之间存在着一一对应关系。这种对应关系分析如下： 若i≥j时，则a~ij~在下三角矩阵中。a~ij~之前i行（从0行到第i-1行）一共有1+2+3…+i=i×(i+1)/2个元素，在第i行上，a~ij~之前恰有j个元素。因此有：

k=i×（i+1）/2+j （0≤k＜n（n+1）/2）

若i<j时，则a~ij~在上三角矩阵中。因为有a~ij~=a~ji~，所以只要交换i和j即可得到：

k=j×（j+1）/2+i （0≤k＜n（n+1）/2）

因此，有：

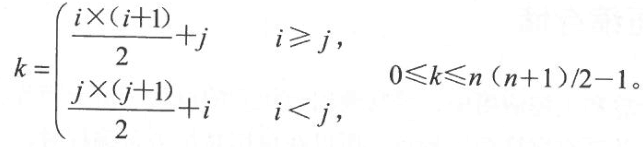
a~ij~的存储地址可用下面的公式计算： LOC(a~ij~)=LOC(sa[k])=LOC(sa[0])+k×d 有了上述的计算公式，就能够立即找到矩阵元素a~ij~在其压缩存储表示sa中的对应位置k。

例如，a~32~和a~23~都存储在sa[8]中，这是因为 k=i×（i+1）/2+j=3x(3+1)/2+2=8

【例】已知d和B是两个阶的对称矩阵，因为是对称矩阵，所以仅需要输入下三角元素值存入一维数组。试写一算法，求对称矩阵A和B的乘积。 分析：如果是两个完整的矩阵相乘，其算法是比较简单的，但由于是对称矩阵，所以要清楚对称矩阵的第i行和第j列的元素数据在一维数组中的位置，其位置计算公式为:

1=i×（i+1）/2+j 当i≥j时（Aij，Bij处于下三角中）

1=j×（j+1）/2+i 当i<j时（Aij，Bij处于上三角中）

其中，1代表A~ij~在其对称矩阵中的位置，而且0≤1≤n ( n+1 )/2。因此，实现本题功能的算法如下：

void matrixmult ( int a[], int b[], int c[] [20], int n){ //n为A、B矩阵下三角元素个数，a,b分别为一维数组，存放矩阵A和B的下三角元素值，c存放A和B的乘积
    for ( i=0; i<20; i++)
        for ( j=0; j<20; j++) {
            s=0;
            for ( k=0; k<n; k++) {
                if ( i>=k ) //表示元素为下三角的元素，计算在a数组中的下标
                    11=i*(i+1)/2+k;
                else //表示元素为上三角的元素，计算下标
                    11=k*(k+1)/2+i;
                if ( k>=j ) //表示元素为下三角的元素，计算在b数组中的下标
                    12=k*(k+1)/2+j;
                else
                    12=j*(j+1)/2+k;
                s=s+a[11]*b[12];
            }
            c[i, j]=s;
        }
}

2.1.2. 三角矩阵

以主对角线划分，三角矩阵有上三角和下三角两种。下三角矩阵正好相反，它的主对角线上方均为常数c或零，如图4.3(a)所示；上三角矩阵是指矩阵的下三角（不包括对角线）中的元素均为常数c或是零的n阶方阵，如图4.3(b)所示。一般情况下，三角矩阵的常数c均为零。

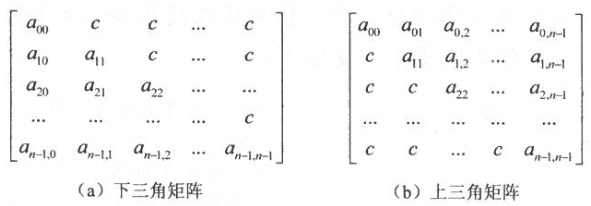
三角矩阵中的重复元素C可共享一个存储空间，其余的元素正好有n(n+1)/2个，因此，三角矩阵可压缩存储在一维数组sa[n(n+1)/2+1]中，其中c存放在数组的最后一个元素中。

在上三角矩阵中，主对角线上第m(0≤m<n)行上恰好有n-m个元素，按行优先顺序存储上三角矩阵中元素a~ij~时，a~ij~之前有i行（0~i-1)，一共有元素个数：

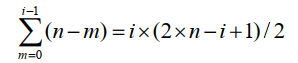
而在第i行，a~ij~之前有~j-i~个元素，因此sa[k]和a~ij~存储位置的对应关系为:

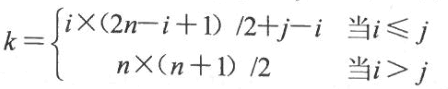
而在下三角矩阵中，sa[k]和a~ij~存储位置对应关系与前面介绍的对称矩阵压缩存储类似，只是在当i<j时，下三角矩阵中仅有一个存储位置。因此，该对应关系为：

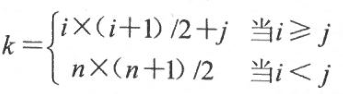
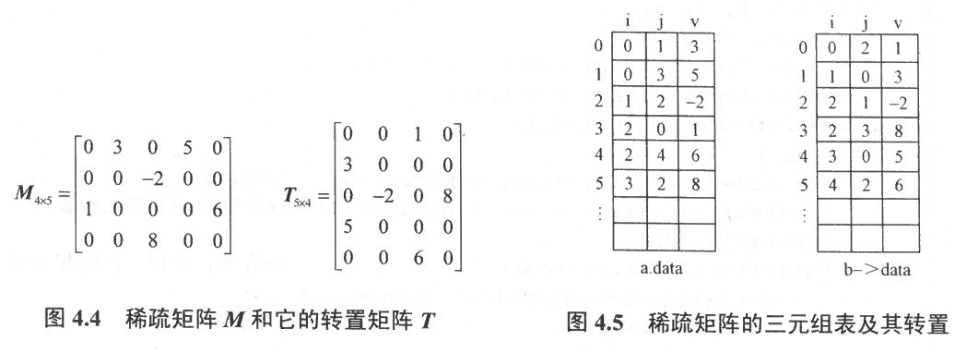
2.2. 稀疏矩阵

由于特殊矩阵中非零元素的分布是有规律的，因此总可以找到矩阵元素与一维数组的下标的对应关系。但还有一种矩阵，其中有个非零元素，而远远小于矩阵元素的总数，通常把这种矩阵称为稀疏矩阵。为了节省存储单元，也可用压缩存储方法只存储非零元素。由于稀疏矩阵非零元素的分布一般是没有规律的，因此在存储非零元素时，除了存储非零元素的值之外，还必须同时存储该元素的行、列位置（即下标），所以可用一个称为三元组（i，j，a~ij~ )来唯一确定一个非零元素。 当用三元组来表示非零元素时，对稀疏矩阵进行压缩存储通常有两种方法：顺序存储和链式存储。链式存储一般采用的是十字链表法，结构比较复杂，在这里就不再介绍，只介绍顺序存储方式的压缩存储技术。

2.2.1. 三元组表

如果将表示稀疏矩阵非零元素的三元组按行优先的顺序排列，则可得到一个其结点均为三元组的线性表，将这种线性表的顺序存储结构称为三元组表。 为了操作方便，对稀疏矩阵的总行数、总列数以及非零元素个数均作为三元组表的辅助属性加以描述。

#define MaxSize 1000 //假设非零元素个数的最大为1000个
typedef struct {
    int i, j; //非零元素的行号、列号（下标）
    DataType v; //非零元素值
} TriTupleNode;
typedef struct {
    TriTupleNode data [ MaxSize ]; //存储三元组的数组
    int m, n, t; //矩阵的行数、列数和非零元素个数
} TSMatrix; //稀疏矩阵类型

【例4.4】试写一个算法，建立顺序存储稀疏矩阵的三元组表。

void CreateTriTable ( TSMatrix * b, int a[][5], int m, int n ){ //建立稀疏矩阵的三元组表
    int i, j, k=0 ;
    for ( i=0; i<m; i++)
        for ( j=0; j<n; j++)
            if ( a[i][j]!=0 ) { //找出非零元素
                b->data[k].i=i; //记录非零元素行下标
                b->data[k].j=j; //记录非零元素列下标
                b->data[k].v=a[i][j]; //保存非零值
                k++; //统计非零元素个数
            }
    b->m=m; b->n=n; //记录矩阵行列数
    b->t=k; //保存非零个数
}

【例4.5】试写一个算法，实现以三元组表结构存储的稀疏矩阵的转置运算。

（1）一般的转置算法 假设a是TSMatrix型变量，表示稀疏矩阵M；b是指向稀疏矩阵T的TSMatrix型指针变量。从上面的分析可知，要将转置成就是将的三元组表a.data转置为T的三元组表b->data。要想得到如图4.5所示的按行优先顺序存储的b->data，就必须重新排列三元组表的顺序。由于M的行是T的列，所以按a.data的列转置，所得到的转置矩阵T的三元组表b->data—定是按行优先顺序存放的。实现这种方法的基本思想是：对M中的每一列col(0≤col≤a.n-1)从头至尾依次扫描三元组表，找出所有列号等于col的那些三元组，并将它们的行号和列号互换后再依次存入b->data中，这样就可得到T的按行优先的三元组表。

3 广义表基础

1. 尚德机构 ↩ ↩